|
Narasingha Das Research Scholar, Dept. of Economics, Vidyasagar University, West Bengal, India. Email- narasinghadas@gmail.com A Time Series Analysis on the Relation between Foreign Direct Investment & Total Factor Productivity Growth of the Indian Organised Manufacturing Sector: 1980-81 to 2010-11 |
This paper attempts to measure productivity performance of the Indian Manufacturing Industry during the period 1980-81 to 2010-11. To measure total factor productivity growth& various other related performance indicators a non-parametric approach, namely, Malmquist Data Envelopment Analysis has been used.A comparative analysis between the pre (1980-81 to 1990-1991)& post liberalisation (1991-92 to 2010-11) era has also been taken up in this study. The paper also seeks to examine the impact of foreign direct investment on the overall total factor productivity growth of the Indian Manufacturing Industry. The present study shows a positive TFP growth for the entire period. But, again, there is a fall in the TFPG from pre to post-liberalisation period.Interestingly, we observed a positive impact of foreign direct investment on total factor productivity growth for the Indian Manufacturing Industries.
Key Words: Indian Manufacturing Industry, Total Factor Productivity, Malmquist index, Data Envelopment Analysis, FDI.
JEL Classification: C14, C32, D24.
The impact on the host economy of investment by multinational enterprises remains an unresolved and debated issue (Aghion et al. 2006, Bitzer and Görg 2005). Some countries and industries benefit significantly from foreign entry in terms of productivity and knowledge spillovers. Others benefit less or are even hurt.
While academics tend to treat FDI as a homogenous capital flow, policy makers, on the other hand, seem to believe that some FDI projects are better than others. National policies toward foreign directinvestment (FDI) seek to attract some types of FDI and regulate other types in a pattern which seems to reflect a belief among policymakers that FDI projects differ greatly in terms of the national benefits to be derived from them. UNCTAD’s World Investment Report 2006 for instance describes “quality FDI” as “the kind that would significantly increase employment, enhance skills and boost the competitiveness of local enterprises.”
While in theory the nexus between FDI and growth (in terms of output and productivity) is in general positive, the empirical literature is far less conclusive. Some studies find positive effects from outward FDI for the investing country (Van Pottelsberghe and Lichtenberg, 2001; Nachum et al., 2000), but suggest a potential negative impact from inward FDI on the host country. This results from a possible decrease in indigenous innovative capacity or crowding out of domestic firms or domestic investment. Thus, in their view and in line with the standard literature on the determinants of FDI (i.e. Dunning’s OLI paradigm, see Dunning 1988) inward FDI is intended to take advantage of host country (locational) characteristics instead of disseminating new technologies originating in the sending country. Other studies report more positive findings: Nadiri (1993) finds positive and significant effects from US sourced capital on productivity growth of manufacturing industries in France, Germany, Japan and the UK. Also Borensztein et al. (1998) find a positive influence of FDI flows from industrial countries on developing countries’ growth. However, they report also a minimum threshold level of human capital for the productivity enhancing impact of FDI, emphasizing the role of absorptive capacity. Absorptive capacity or minimum threshold levels in a country’s ability to profit from inward FDI is often mentioned in the literature (see also Blomström et al. 1996). Consequently the effect of FDI depends among other things to a large extent on the characteristics of the country that receives FDI. However, the resulting issue of cross-country heterogeneity has largely been neglected in the literature so far with few exceptions. Blonigen and Wang (2005) stress explicitly cross-country heterogeneity as the crucial factor which determines the effect of FDI on growth. Further, Nair-Reichert and Weinhold (2001) and Mayer-Foulkes and Nunnenkamp (2005) explicitly take up this aspect in their analysis. Our paper will follow their direction and introduce two forms of heterogeneity, differences between countries and differences between receiving industries.
We argue that since host country heterogeneity plays a role, it is equally likely that the impact of FDI on the host economy differs greatly according to the receiving industry. FDI in constant returns to scale industries will have different effects than FDI in increasing returns to scale industries. Likewise, the effect of FDI may be related to the technology and human capital intensity of the industry and other factors. As a very intuitive example, heavy FDI in the extractive sector in Nigeria has not improved the country’s growth performance (Akinlo, 2004). Consequently, the potential for positive spillovers does not solely depend on a country’s overall absorptive capacity, but also on which sectors or industries in the economy receive FDI. Thus, the impact of FDI differs depending on country specific absorptive capacity or stage of development as well as on the sectoral and industrial structure and allocation of FDI. Since the two are in general related, this implies a relationship between the industrial pattern of inward FDI and its effect on the host country. The economy wide effect of industry specific FDI inflows will then further depend on the extent of intra-industry versus inter-industry spillovers.
The concept of technical efficiency indicates the degree of success in the utilization of productive resources. Technical efficiency is considered to be an important determinant of productivity growth and international competitiveness in any economy (Taymaz and Saatci, 1997). There are different schools of thought in estimating the technical efficiency. Technical efficiency consists of maximizing the level of production that can be obtained from a given combination of factors. In the Indian context, number of studies examined the technical efficiency of the manufacturing industry, e.g., Page (1984), Little et al. (1987), Patibandla (1998), Mitra (1999), Agarwal (2001), and Mitra et al. (2002), Bhandari et al. (2007a, 2007b) and many others. Krishna and Mitra (1998) investigated the effects on competition and productivity of the dramatic 1991 trade liberalization in case of Indian manufacturing industries. Using firm-level data from a variety of industries, they find some evidence of an increase in the growth rate of productivity. Driffield and Kambhampati (2003) estimate frontier production functions for six manufacturing industries. Their findings suggest an increase in overall efficiency in five out of the six manufacturing industries in the post-reform period. Mukherjee and Ray (2005) examined the efficiency dynamics of a ‘typical’ firm in individual states during the pre and post-reform period. Their findings establish no major change in the efficiency ranking for different states after the reforms was initiated. Using a panel dataset of 121 Indian manufacturing industries from 1981 to 1998, Pattnayak and Thangavelu (2005) find evidence of total factor productivity improvements for most of the industries after the reform period.
While the 1991 economic reform was radical, India adopted a gradualist approach to reform, meaning a frustratingly slow pace of implementation (Ahluwalia, 2002). It suggests that it is more appropriate to examine the effect of liberalization on manufacturing sectors’ efficiency using a longer time span for both pre and post-reform. How did this economic reform program shifted Indian manufacturing into global stage and influencing technical and scale economies of major industries? In answering this question, we employ a nonparametric approach in explaining productivity changes, technical progress and scale efficiencies of industries within the sector. In this paper, we examine the impact of liberalization on the technical efficiency of Indian Manufacturing industry by comparing pre and post economic reform periods.
Analysis of technical efficiency of manufacturing industries in developing countries has received considerable attention in the economic literature in recent years. Recent literature includes Onderet al. (2003) for Turkey, Pham et al. (2009) for Vietnam, Margonoet al. (2010) for Indonesia, and Mastromarco (2008) for developing countries among others. Technical efficiency is concerned with how closely the production unit operates to the frontier for the production possibility set. The historical roots of a rigorous approach to efficiency measurement can be traced to the works of Debreu (1951) and Farrell (1957). Over the past three decades, a variety of approaches, parametric and non-parametric, have been developed to investigate the failure of producers to achieve the same level of efficiency. For a detailed survey on such methodologies, see Kalirajan and Shand (1999). In parametric models, one specifies an explicit functional form for the frontier and econometrically estimates the parameters using sample data for inputs and output, and hence the accuracy of the derived technical efficiency estimates is sensitive to the nature of the functional form specified. In contrast, the method of Data Envelopment Analysis (DEA) introduced by
Charneset al. (1978) and further generalized by Banker et al. (1984) offers a non-parametric alternative to parametric frontier production function analysis. A production frontier is empirically constructed using linear programming methods from observed input-output data of sample decision making units (DMUs). In this study, we adopt the output-oriented (OO) DEA that seeks the maximum proportional increase in output production, with input levels held fixed. Lovell (1996) gives a clear description of how the DEA based Malmquist approach implements such decomposition.
In this regard, to judge the relation between the total factor productivity growth (TFP) and foreign direct investment (FDI), though there is a lack of literature, we reviewed some important works which expose the relation between these two factors for other countries.
In a first set of studies, the relation between FDI and industrial growth is analysed at a city (Démurger 1996a, Wei 1994 and 1996) or a provincial level (Démurger 1996b and 2000, Modyand Wang 1997).
Wei (1994), shows that between 1988 and 1990 the level of FDI contributed more to differences in nominal industrial output than did exports. He specifically notes that such investment results in a spill-over oftechnological and managerial know-how between firms in the same city.
Moreover, Wei (1996) finds that a 1 percent increase in the share of FDI in relation with industrial output in 1988 has been associated with a 0.32 percent higher growth rate in output between 1988 and 1990 and that about 20% of the difference between the cities’ output growth could be explained by the difference in the share of FDI’s in output.
Démurger (1996a) confirms,within an augmented production function framework, the predominant short-term impact of FDI in annual average growth rates of real industrial output. Moreover, the paper not only points out the overall predominance of FDI but also indicates that in the short run, the contribution of FDIto industrial growth tends to dominate, and even replace, that of exports. It also tests whether the influence of export growth on industrial growth depends upon the relative size of foreigninvestment. Results indicate that the marginal effect of export growth on industrial growth is reduced where FDI is relatively high and thus suggest that FDI could have been a substitute to exports as a growth factor, at least at the end of the 80s.
At a provincial level, Démurger (1996b) investigates the relation between industrial growth and opening-up for 19 provinces over the 1983-92 period. The results show that i) both FDI and exports have a positive contribution to industrial productivity and that, at least in the short term, FDI has a higher contribution than exports and that ii) FDI has a positive effect on the domestic accumulation of capital. It indeed explains almost half of the variations in total investment and does not appear as a substitute for domestic capital, but rather as a stimulus. The hypothesis of a crowding-out effect on domestic investment can thus be rejected for the studied period.
Furthermore, Démurger (2000) gives an explanation of the economic growth of Chinese provinces up to the mid-90s based on the dynamics between FDI and growth, as well as on a dynamics due to the geographical propagation of growth itself. The evaluation of the interdependence of growth between Chinese provinces and, within provinces, between cities gives an additional explanation for the Chinese growth process since inter-provincial propagation of growth reinforces the dynamism of coastal provinces, but also contributes to the overall growth process.
Finally, using sector data, Mody and Wang (1997) also show that FDI – as a percentage of population – has a significant impact in the short-term on industrial output growth. However,they also observe that the effect of FDI tends to decrease in a longer term. Their interpretation of this result is that in the short-term, FDI is the most mobile factor and is therefore a dominant driving force for growth. On the other hand, over the longer term, variables such as education and infrastructure respond to the rise in demand for complementary assets and the contribution of FDI diminishes. Finally, they underline the fact that the effectiveness of education is enhanced when it is associated with the foreign expertise that accompanies investment.
Another part of the empirical literature on the role of FDI in industry focuses on the relative efficiency of foreign-funded firms and their impact on domestic firms.
Within this literature, the research work carried out by Sun (1998) provides an extensive assessment of FDI impact on China’s economy, and more precisely on industry. Sun (1998, chapter 5) notably highlights the differences between the characteristics and performances of FIEs and those of domestic firms, especially SOEs. FIEs have a higher capital intensity than domestic firms do in all sectors, indicating a higher technology content of the production process. Moreover, the investigation of productive efficiency in different categories of firms, carried out on the basis of the 1995 Census data, shows that the average productivity of both labour and capital in FIEs is respectively 2.8 and 2.2 times higher than that of State-owned enterprises. It also shows that the elasticity of output with regard to labour and capital is greater in FIEs than in SOEs, thus suggesting a better technical and management efficiency.
In a similar perspective, Fan (1999, chapter 5) gives estimations of total factor productivity (TFP) growth by ownership categories (state-owned, collective and foreign-funded enterprises). Using industrial level data on 28 manufacturing industries for 20 provinces throughout the 1993-95 period, she particularly shows that the “foreign category” experienced the highest TFP growth (with an average of 4.9 % per year), the gap between domestic and FDI firms being higher in capital intensive industries. Furthermore, investigating the issue of technological spill-over from foreign to domestic firms, Fan (1999, chapter 7) shows that positive andsignificant spill-over appears only in industries “which are mainly labour-intensive and have alow to moderate technology gap between Chinese and foreign firms” (p. 169).
In a comparative perspective too, Zhang and Zheng (1998) carry out an investigation centred on the impact of multinational enterprises (MNEs) on industrial structure and efficiency. They note that since 1992 the pattern of FDI inflows has undergone significant changes, due to the fact that MNEs have massively entered the Chinese market and initiated a structural adjustment in the form of a reallocation of resources from labour intensive to more capital intensive sectors. They compare the performance of a selected sample of MNEs’ affiliates in China with that of all enterprises and other FIEs on the basis of the 1995 census. MNEs’ affiliates are found to be more profitable (profit/sales) and less export-oriented than other FIEs. Compared to all industrial firms and to all FIEs, their production is more concentrated in the sectors with the highest degree of capital intensity (assets per capita). Their distribution across sectors shows that they are relatively specialised in transport equipment, electric and electronic goods. Estimating the statistical relation between several structural variables, and the sector distribution of MNEs and large and medium-sized domestic enterprises, the study finds a positive correlation between the share of MNEs in sales and labour productivity, profitability, average wage, the level of education of employees, R&D expenditures, concentration ratio and size effects. Although these relations do not give any information about the direction of causation, they suggest that marginal changes in MNEs sales share will be associated with an increase in the related variables.
The in-depth analysis of the determinants of technical efficiency in Chinese manufacturingindustries, made by Sun et al. (1999), confirms the observation of a higher efficiency in FIEs.Using the Data Envelopment Analysis approach (DEA), Sun et al. (1999) compute technical efficiency scores for 28 manufacturing industries across 29 provinces in 1995 and compare them across sectors and provinces. The industry-based comparison indicates that on average,textile, timber processing and non-ferrous metal industries have lower technical efficiency scores while the provincial comparison shows that the most efficient provinces are on average coastal ones. Sun et al. then look at the determinants of technical efficiency differentials across provinces and industries and find some evidence on the role of economic openness. Their results thus generally confirm the positive relationship between economic openness, measured either by the export-output ratio or the share of FDI in total equity, and technical efficiency in light manufacturing industries located in the coastal region (rather than in hinterland).
The presence of FIEs has thus a direct positive effect on industrial performance. As shown by Sun (1998, chapter 6), FIEs also have indirect effects through their linkages with domestic sectors. According to this investigation, FIEs are located in industrial sectors which have high backward linkage indices and output multipliers (as derived from input-output table of China in 1992) and thus, have strong potential linkage effects on the domestic economy. FIEs, which are now important industrial producers, contribute to the growth of the domestic sectors through their input demand to domestic firms. The case studies of car industry and electronic sectors confirm this observation as they show the relatively high local content of inputs used in FIEs.
The localisation of inputs in major automobile FIEs has considerably increased in the 90s (and reached 80% in Shanghai Volkswagen in 1993). In electronic industry, the top ten FIEs also show high rates of input localisation. The localisation rates are generally higher in TVproduction, and lower in more technically complex products, indicating that there is still scopefor improving the technological capacities of domestic firms.
Finally, the analysis made by Wu (2000) on 10 coastal provinces over the period from 1983 to 1995 gives a complementary view of the temporal evolution of FDI efficiency. The performance indicator for FDI, derived from a production frontier method, particularly shows a few interesting patterns. First, for all provinces, it follows an increasing trend over time, which indicates that while FDI efficiency was relatively poor in the 80s, it has improved and converged across the 10 provinces during the 90s. By 1995, all coastal provinces thus tendedto use foreign capital rather efficiently. Second, on a province-to-province basis, Shanghai appears as the best performer in terms of FDI efficiency since the late 80s.
McKinsey, 2005, argued that the US automotive industry is a sector that was significantly exposed to foreign competition and benefited from it recently. The Big Three’s responses to competitive threats from Japanese, German and Korean manufacturers were largely responsible for increases in sector labor productivity in 1987-2002. Rising 3.3% a year in the period, productivity growth in the US production of new vehicles was substantially faster than 2.1% growth rate achieved by the non-farm business sector. Process improvements, most notably changes in physical plants necessary for adoption of “lean production”, were responsible for almost half of productivity growth1, although it took 10-15 years for the Big Three to implement the new methods. While capital deepening accounted for only 10% of productivity growth in 1987-1996, it caused 60% of that growth in 1997-2002.
The experience of the Czech electronics industry was different. In many ways it didn’t benefit from the entry of world-class players such as Philips and Panasonic. These companies largely undertook contract manufacturing and invested little in R&D. The R&D intensity of foreign affiliates is substantially lower than that of domestic firms and below the average for the Czech manufacturing. For the economy as a whole, foreign ownership was found to have a significant negative impact on propensity to conduct R&D (UNCTAD, Srholec 2005).
Long run growth can only be increased through technological and population growth and if FDI positively influences technology, then it will be growth advancing (Solow 1956).
Somwaru and Makki (2004) indicate that according to recent endogenous growth theory, FDI can be growth advancing if it results in increasing returns in production through spillover and technological transfers via diffusion processes.
In addition, Easterly et al. (1995) argue that technology transfer depends on the diffusion process and that can take place through four modes: transfer of new technologies and ideas; high technology imports; foreign technology adoption; and level of human capital.
Findlay (1978) presents the contagion effect of managerial practices and advanced technology introduced by foreign firms on the host country’s technology.
A recent study by Banga (2005) demonstrates that FDI, trade and technological progress have differential impact on wages and employment. While higher extent of FDI in an industry leads to higher wage rate in the industry, it has no impact on its employment. On the other hand, higher export intensity of an industry increases employment in the industry but has no effect on its wage rate. Technological progress is found to be laboursaving but does not influence the wage rate. Further, the results show that domestic innovation in terms of research and development intensity has been labor utilizing in nature but import of technologyhas unfavorably affected employment in India. Rajit Kumar Sahoo (2005) has pointed out that FDI has a direct and indirect impact and on a certain particular sectors of the economy. A study on the impact of FDI on manufacturing sector reveals that FDI inflows in chemicals, electrical and electronics shows direct impact and FDI inflow in drugs and pharmaceutical sectors shows indirect impact (spillover effects). FDI is an important vehicle for the transfer of technology and knowledge and it demonstrates that it can have a long run effect on growth by generating increasing return in production via positive externalities and productive spill overs. Thus, FDI can lead to a higher growth by incorporating new inputs and techniques (Feenstra and Markusen, 1994).
In this backdrop, our study is an attempt to find out the relationship between FDI and the total factor productivity growth for the overall Indian manufacturing industries. Presently, when we survey the literature on this relationship, we find that there is a dearth of literature on this particular aspect for Indian case. So, our study makes an attempt to fill the gap in the existing literature.
The major objectives of our study are:
Section 2 deals with the methodological issues. Section 3 analyses the results obtained.. Lastly, Section 4 deals with summary & conclusion of our study.
2.1. Model Of TFPG Estimation:
Description of Data & Measurement of Variables:
The present study is based on manufacturing industry-level time series data taken from several issues of Annual Survey of Industries, National Accounts Statistics, CMIE and Economic Survey, Statistical Abstracts (several issues), RBI bulletin etc. covering a period of 31 years commencing from 1980-81 to 2010-11. Selection of time period is largely guided by availability of data. The entire period is sub-divided into two phases as 1980-81 to 1990-91, 1991-92 to 2010-11 (Pre-reform phase and Post-reform phase). Sub-divisions of total period is being taken logically as such to assess conveniently the impact of reforms on total factor productivity growth and employment.
Now, output in this context is measured as real gross value added index. The GDP deflator has been used as the deflator of gross value added.
In this study Labour index is formed as a weighted sum of number of heads in two groups (Workers & Other employees), weights being the relative group remunerations. Relevant data is obtained from ASI & Indian Labour Statistics.
So far as capital input is concerned, we have taken into account the perpetual inventory method. In our study, real gross fixed capital stock is taken as the measure of capital input. Deflator used is obtained from data on GFCF at current and constant prices. Data for the above purpose are obtained from various issues of ASI & NAS published by CSO, Govt. of India.
Now, as discussed earlier in the literature section, FDI is an important vehicle for the transfer of technology and knowledge and it demonstrates that it can have a long run effect on growth bygenerating increasing returns in production via positive externalities and productive spillovers. Thus, FDI can lead to a higher growth by incorporating new inputs and techniques. Technology transfer through FDI depends on the diffusion process that can take place through four modes: transfer of new technologies and ideas; high technology imports; foreign technology adoption; and level of human capital. So it is quite natural that based on these four modes there may be enhancement of the total factor productivity growth for the manufacturing industries. The data on foreign direct investment (FDI) is obtained from Secretariat of Industrial Assistance (SIA’s), several issues, published by the Department of Industrial Policy & Promotion, Govt. of India, Ministry of Commerce & Industry.
Econometric Specification:
The conventional setup of Färeet al. (1992) is adopted in modelling the problem as transformation of a vector of inputs xt∈ into a vector of output yt∈ .The production technology at each time period t, denoted St, is identified as the set of all technologically feasible input-output combinations at time t (Lovell, 1996). It is constructed from the data as:


The term outside the brackets shows the change in technical efficiency while the geometric mean of the two ratios inside the brackets measures the shift in technology between the two period ‘t’ & ‘t+1’; this could be called technological progress. So :
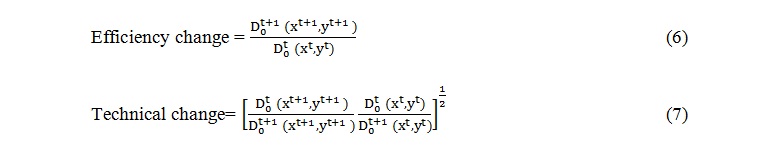
In each of the formulas i.e., equation (6) & (7), a value greater than one indicates a positive growth of TFP (an improvement) from a period ‘t’ to ‘t+1’ and a value smaller than one represents deteriorations in performance over time.
We can decompose the total factor productivity growth in following way as well:
MTFPI = Technical Efficiency change X Technical Change
(Catching up effect) (Frontier effect)
MTFPI is the product of measure of efficiency change (catching up effect) at current period ‘t’ and previous period ‘s’ (average geometrically) and a technical change (frontier effect) as measured by shift in a frontier over the same period. The catching up effect measures that a firm is how much close to the frontier by capturing extent of diffusion of technology or knowledge of technology use. On the other side frontier effect measures the movement of frontier between two periods with regards to rate of technology adoption. In DEA-Malmquist TFP Index does not assume all the firms or sectors are efficient so therefore any firm or sector can be performing less than the efficient frontier. In this methodology we will use the output oriented analysis because most of the firms and sectors have their objective to maximize output in the form of revenue or profit. It is also assumed that there is constant return to scale (CRS) technology to estimate distance function for calculating Malmquist TFP index and if technology exhibits constant return to scale (CRS), the input based and output based Malmquist TFP Index will provide the same measure of productivity change.
2.2. Time Series Econometric tests to assess the nature of the relationship between TFP and FDI:
Step – I: The Stationarity Test (Unit Root Test):
It is suggested that when dealing with time series data, a number of econometric issues can influence the estimation of parameters using OLS. By regressing a time series variable on other time series variables using OLS estimation can result in a very high R2, although there is no meaningful relationship between the variables. This situation reflects the problem of spurious regression between totally unrelated variables generated by a non-stationary process. Therefore, prior to testing Cointegration and implementing the Granger Causality test, econometric methodology needs to examine the stationarity; for each individual time series. Most macroeconomic data are non-stationary, i.e., they tend to exhibit a deterministic and/or stochastic trend. Therefore, it is recommended that a stationarity (unit root) test be carried out to test for the order of integration. A series (Xt) is said to be stationary if the mean and variance are time-invariant. A non-stationary time series will have a time dependent mean or make sure that the variables are stationary, because if they are not, the standard assumptions for asymptotic analysis in the Granger test will not be valid. Therefore, a stochastic process that is said to be stationary simply implies that the mean [E(Xt)] and the variance [var (Xt)] of X remain constant over time for all t, and the covariance [cov(Xt, Xs)] i.e., the correlation between any two values of X taken from different time periods depends on the difference apart in time between the two values for all t≠s. Since standard regression analysis requires that data series be stationary, it is obviously important that we first test for this requirement to determine whether the series used in the regression process is a difference stationary or trend stationary.
To test the stationary of the variables, we use the Augmented Dickey Fuller (ADF)test, Phillips-Perron Unit Root Test&Dickey Fuller test with GLS detrending.
Now, once the number of unit roots in the series is decided, the next step before applying Johansen’s (1988) cointegration test is to determine an appropriate number of lags to be used in estimation since the choice of lag length is crucial in the Johansen procedure. In selection of appropriate lag length, standard literature follows either Akaike Information Criteria (AIC) or Bayesian Information Criteria (BIC) which is also known as Schwarz Information Criteria (SIC) or both. In our study, the appropriate lag length is selected on the basis of Schwarz Information Criteria (SIC) as we are more interested to identify the true model rather than to find out the best approximating model to the unknown data generating process which AIC actually gives (Henry de-Graft Acquah, 2009). Another reason is that, AIC does not depend directly on sample size. Bozdogan (1987) noted that because of this, AIC lacks certain properties of asymptotic consistency. Although BIC takes a similar form like AIC, it is derived within a Bayesian framework, reflects sample size and have properties of asymptotic consistency. For reasonable sample sizes, BIC apply a larger penalty than AIC, thus other factors being equal it tend to select simple models than does AIC. From a Bayesian view point this motivates the adoption of the Bayesian information criteria. Bickel & Zhang (1992) & Zhang (1993) demonstrate that BIC is consistent whilst in contrast AIC is not.
Step – II:The Cointegration Test
Regression on non stationary variables is permitted if their linear combination is stationary. It has been recognized in recent literature that if a linear combination of integrated variables is stationary then such variables are said to be cointegrated. Although Engle and Granger (1987) was the first to introduce the cointegration test, the tests propounded by Stock and Watson (1988), Johanson (1991) and Johansen and Juselius (1990) are more useful in testing the long run equilibrium relationships in multivariate setting.
Step III: The Granger Causality Test:
Causality is a kind of statistical feedback concept which is widely used in the building of forecasting models. Historically, Granger (1969) and Sim (1972) were the ones who formalized the application of causality in economics. Granger causality test is a technique for determining whether one time series is significant in forecasting another (Granger, 1969). The standard Granger Causality Test (Granger, 1988) seeks to determine whether past values of a variable helps to predict changes in another variable. The definition states that in the conditional distribution, lagged values of Yt add no information to explanation of movements of Xt beyond that provided by lagged values of Xt itself (Green, 2003). We should take note of the fact that the Granger causality technique measures the information given by one variable in explaining the latest value of another variable. In addition, it also says that variable Y is Granger caused by variable X if variable X assists in predicting the values of variable Y. if this is the case, it means that the lagged values of variable X are statistically significant in explaining variable Y. The null hypothesis (H0) that we test in this case that X variable does not Granger cause variable Y and variable Y does not Granger cause variable X.
In this section, we have calculated total factor productivity growth and its component using Malmquist Productivity Index under two inputs- labour & capital and one output framework. Estimation of annual TFP growth rate of Indian manufacturing industries for the pre as well as post-reform period at aggregate level are presented in Table: 1, Table: 2 & Table: 3 respectively.
|
Year |
EFFCH |
TECHCH |
PECH |
SECH |
TFPCH |
|
1980-81 |
- |
- |
- |
- |
- |
|
1981-82 |
1.000 |
1.177 |
1.000 |
1.000 |
1.177 |
|
1982-83 |
1.000 |
0.974 |
1.000 |
1.000 |
0.974 |
|
1983-84 |
1.000 |
1.088 |
1.000 |
1.000 |
1.088 |
|
1984-85 |
1.000 |
0.923 |
1.000 |
1.000 |
0.923 |
|
1985-86 |
1.000 |
1.017 |
1.000 |
1.000 |
1.017 |
|
1986-87 |
1.000 |
0.947 |
1.000 |
1.000 |
0.947 |
|
1987-88 |
1.000 |
1.083 |
1.000 |
1.000 |
1.083 |
|
1988-89 |
1.000 |
1.004 |
1.000 |
1.000 |
1.004 |
|
1989-90 |
1.000 |
1.146 |
1.000 |
1.000 |
1.146 |
|
1990-91 |
1.000 |
1.039 |
1.000 |
1.000 |
1.039 |
|
1991-92 |
1.000 |
1.110 |
1.000 |
1.000 |
1.110 |
|
1992-93 |
1.000 |
1.038 |
1.000 |
1.000 |
1.038 |
|
1993-94 |
1.000 |
0.918 |
1.000 |
1.000 |
0.918 |
|
1994-95 |
1.000 |
1.361 |
1.000 |
1.000 |
1.361 |
|
1995-96 |
1.000 |
1.014 |
1.000 |
1.000 |
1.014 |
|
1996-97 |
1.000 |
0.973 |
1.000 |
1.000 |
0.973 |
|
1997-98 |
1.000 |
0.917 |
1.000 |
1.000 |
0.917 |
|
1998-99 |
1.000 |
0.954 |
1.000 |
1.000 |
0.954 |
|
1999-2000 |
1.000 |
0.798 |
1.000 |
1.000 |
0.798 |
|
2000-01 |
1.000 |
0.871 |
1.000 |
1.000 |
0.871 |
|
2001-02 |
1.000 |
1.149 |
1.000 |
1.000 |
1.149 |
|
2002-03 |
1.000 |
0.879 |
1.000 |
1.000 |
0.879 |
|
2003-04 |
1.000 |
1.112 |
1.000 |
1.000 |
1.112 |
|
2004-05 |
1.000 |
1.211 |
1.000 |
1.000 |
1.211 |
|
2005-06 |
1.000 |
1.197 |
1.000 |
1.000 |
1.197 |
|
2006-07 |
1.000 |
1.040 |
1.000 |
1.000 |
1.040 |
|
2007-08 |
1.000 |
1.024 |
1.000 |
1.000 |
1.024 |
|
2008-09 |
1.000 |
0.996 |
1.000 |
1.000 |
0.996 |
|
2009-10 |
1.000 |
0.949 |
1.000 |
1.000 |
0.949 |
|
2010-11 |
1.000 |
0.902 |
1.000 |
1.000 |
0.902 |
|
Mean |
1.000 |
1.020 |
1.000 |
1.000 |
1.020 |
Source: Authors own estimates by using DEAP software, version 2.1
From Table-1, we find that the annual average TFPG for the Indian manufacturing sector for the entire period under study (1980-81 to 2010-11) is positive and it is 2.0. From Table-2, for the pre-reform period (1980-81 to 1990-91) the annual average TFPG is also positive and it is 3.70.
|
Year |
EFFCH |
TECHCH |
PECH |
SECH |
TFPCH |
|
1980-81 |
- |
- |
- |
- |
- |
|
1981-82 |
1.000 |
1.177 |
1.000 |
1.000 |
1.177 |
|
1982-83 |
1.000 |
0.974 |
1.000 |
1.000 |
0.974 |
|
1983-84 |
1.000 |
1.088 |
1.000 |
1.000 |
1.088 |
|
1984-85 |
1.000 |
0.923 |
1.000 |
1.000 |
0.923 |
|
1985-86 |
1.000 |
1.017 |
1.000 |
1.000 |
1.017 |
|
1986-87 |
1.000 |
0.947 |
1.000 |
1.000 |
0.947 |
|
1987-88 |
1.000 |
1.083 |
1.000 |
1.000 |
1.083 |
|
1988-89 |
1.000 |
1.004 |
1.000 |
1.000 |
1.004 |
|
1989-90 |
1.000 |
1.146 |
1.000 |
1.000 |
1.146 |
|
1990-91 |
1.000 |
1.039 |
1.000 |
1.000 |
1.039 |
|
Mean |
1.000 |
1.037 |
1.000 |
1.000 |
1.037 |
Source: Authors own estimates by using DEAP software, version 2.1
|
Year |
EFFCH |
TECHCH |
PECH |
SECH |
TFPCH |
|
1991-92 |
1.000 |
1.110 |
1.000 |
1.000 |
1.110 |
|
1992-93 |
1.000 |
1.038 |
1.000 |
1.000 |
1.038 |
|
1993-94 |
1.000 |
0.918 |
1.000 |
1.000 |
0.918 |
|
1994-95 |
1.000 |
1.361 |
1.000 |
1.000 |
1.361 |
|
1995-96 |
1.000 |
1.014 |
1.000 |
1.000 |
1.014 |
|
1996-97 |
1.000 |
0.973 |
1.000 |
1.000 |
0.973 |
|
1997-98 |
1.000 |
0.917 |
1.000 |
1.000 |
0.917 |
|
1998-99 |
1.000 |
0.954 |
1.000 |
1.000 |
0.954 |
|
1999-2000 |
1.000 |
0.798 |
1.000 |
1.000 |
0.798 |
|
2000-01 |
1.000 |
0.871 |
1.000 |
1.000 |
0.871 |
|
2001-02 |
1.000 |
1.149 |
1.000 |
1.000 |
1.149 |
|
2002-03 |
1.000 |
0.879 |
1.000 |
1.000 |
0.879 |
|
2003-04 |
1.000 |
1.112 |
1.000 |
1.000 |
1.112 |
|
2004-05 |
1.000 |
1.211 |
1.000 |
1.000 |
1.211 |
|
2005-06 |
1.000 |
1.197 |
1.000 |
1.000 |
1.197 |
|
2006-07 |
1.000 |
1.040 |
1.000 |
1.000 |
1.040 |
|
2007-08 |
1.000 |
1.024 |
1.000 |
1.000 |
1.024 |
|
2008-09 |
1.000 |
0.996 |
1.000 |
1.000 |
0.996 |
|
2009-10 |
1.000 |
0.949 |
1.000 |
1.000 |
0.949 |
|
2010-11 |
1.000 |
0.902 |
1.000 |
1.000 |
0.902 |
|
Mean |
1.000 |
1.012 |
1.000 |
1.000 |
1.012 |
Source: Authors own estimates by using DEAP software, version 2.1
Table-3 represents the annual average TFPG of the Indian Manufacturing industries and it is 1.2. Therefore we can say that there is a fall in the TFPG from pre to post reform period. This results reveals that decline in the industry’s TFPG is due to its productivity based frontier capability.
3.2 Empirical results from the causal relationship between change in foreign direct investment and change in total factor productivity growth for the Indian Manufacturing Industry:-
From unit root testing, we have the following results as presented in Table 3.2.1, 3.2.3& 3.2.4.
Table 3.2.1: Results from ADF Unit Root Test
|
Variables |
Intercept Only |
Trend & Intercept |
||
|
Level |
1st Difference |
Level |
1st Difference |
|
|
ΔTFP |
-5.031369* |
-9.610398* |
-4.944927* |
-9.432294* |
|
ΔFDI |
-1.921073 |
-4.308293* |
-1.635656 |
-5.240784* |
Source: Authors own estimate. (*, **, *** represents the significance level at 1%, 5% & 10% respectively)
The result of ADF unit root tests is presented in Table-3.2.1. Each variable is tested in their level & first difference with intercept only and trend & intercept. It is found that the null hypothesis of unit roots cannot be rejected at conventional significance levels for FDI. Therefore it can be concluded that all series are stationary at level i.e., all the series are I(1). For the ADF test, the optimum lag selection is based on Schwartz Information Criterion. Table 3.2.2 suggest that the appropriate lag length is 2 for the total factor productivity and for FDI the appropriate lag length is 1.
Table 3.2.2: Selection of Appropriate Lag Length by SIC
|
Lags |
SIC |
|||
|
ΔTFP |
ΔFDI |
|||
|
Intercept Only |
Trend & Intercept |
Intercept Only |
Trend & Intercept |
|
|
1 |
0.594739 |
0.479411 |
4.745224* |
4.803730* |
|
2 |
0.472002* |
0.350986* |
4.904462 |
4.969009 |
Source: Authors own estimate
The asterisks (*) in the table 3.2.2 indicates the best (that is, minimized) values of the SIC.
Table 3.2.3: Results from Phillips-Perron Unit Root Test
|
Variables |
Intercept Only |
Trend & Intercept |
||
|
Level |
1st Difference |
Level |
1st Difference |
|
|
ΔTFP |
-5.052008* |
-9.610398* |
-4.971133* |
-9.432214* |
|
ΔFDI |
-1.906710 |
-10.39929* |
-4.333240* |
-17.86455* |
Source: Authors own estimate. (*, **, *** represents the significance level at 1%, 5% & 10% respectively)
The result of Phillips-Perron unit root tests is presented in Table-3.2.3. Each variable is tested in their level & first difference with intercept only and trend & intercept. It is found that the null hypothesis of unit roots cannot be rejected at conventional significance levels for FDIs. Thus it can be concluded that all series are stationary at level i.e., all the series are I(1).
Table 3.2.4: Results from DF- GLS detrending Unit Root Test
|
Variables |
Intercept Only |
Trend & Intercept |
||
|
Level |
1st Difference |
Level |
1st Difference |
|
|
ΔTFP |
-4.598083* |
-7.565914* |
-4.862391* |
-9.102501* |
|
ΔFDI |
-0.975706 |
-5.936419* |
-1.249187 |
-5.948666* |
Source: Authors own estimate. (*, **, *** represents the significance level at 1%, 5% & 10% respectively)
The result of DF-GLS detrending unit root tests is presented in Table-3.2.4. Each variable is tested in their level, first difference and second difference with intercept only and trend & intercept. It is found that the null hypothesis of unit roots also cannot be rejected at conventional significance levels for the ΔFDI. Therefore it can be concluded that all series are stationary at their level i.e., all the series are I(1).
Results from Cointegration Test:
Having established the time series properties of the data, the test for presence of long-run relationship between the variables using the Johansen Cointegration test is conducted. The Johansen approach can determine the number of cointigration vectors for any given number of non-stationary variables of the same order. The results reported in Table-3.2.5.suggests that the null hypothesis of no cointegrating vectors can be rejected at 1% level of significance. It can be seen from the trace statistics that we have one co-integration equation at both 1% and 5% level.
Table 3.3.5: Johansen Cointegration Test Results
|
||||||||||||||||||||||||||||||||||||||||
From Johansen Co integration test result the normalized co integration equation can be written as:
ΔTFP= 2.768683 + 0.619896 ΔFDI
(3.12*) (2.91*)
From the above normalized cointegration equation we can say that one unit change in FDI leads to 0.62 unit change in TFP for the Indian Manufacturing industry. t-statistics are given in the parenthesis which are also significant at l% (*) level of significance. Thus we can say that there is a long-run relationship between total factor productivity growth and foreign direct investment for the Indian manufacturing industries.
Findings from Granger Causality Test:
The results of Pair wise Granger Causality between ΔTFP and ΔFDI for the Indian Manufacturing industry are presented in Table-3.2.6. The results reveal that there is a unidirectional causal relationship between change in TFP and change in FDI. Our result confirms that change in FDI is the Granger cause of change in TFP at lag 2, 3 & 4.
Table 3.2.6: Granger Causality test Results
|
Null Hypothesis |
Lag |
Observations |
F-Statistics |
Probability |
Decision |
|
ΔFDI does not Granger Cause Real wage rate ΔTFP |
1 |
30 |
1.1007 |
0.1590 |
Accept |
|
2 |
29 |
4.8999 |
0.0216 |
Reject |
|
|
3 |
28 |
4.20891 |
0.0281 |
Reject |
|
|
4 |
27 |
4.10091 |
0.0298 |
Reject |
|
|
ΔTFP does not Granger Cause ΔFDI |
1 |
30 |
0.08902 |
0.7270 |
Accept |
|
2 |
29 |
0.40231 |
0.6501 |
Accept |
|
|
3 |
28 |
0.37881 |
0.8289 |
Accept |
|
|
4 |
27 |
0.91890 |
0.1771 |
Accept |
Source: Authors own estimate.
The following are the major findings of our study:
First, the result on the overall productivity displays a declining trend of MTFPG in post reform period as compared to pre reform period for the Indian Manufacturing industry. Therefore, it may be concluded that the liberalization policies has its adverse impact on the overall Indian manufacturing industry’s TFP growth.
Second, our result also confirms a significant causal and long-run relationship between foreign direct investment and total factor productivity for the Indian Manufacturing industry. The direction of causality is from FDI to real TFP growth.
Therefore, FDI act as an ingredient of total factor productivity growth for the Indian Manufacturing Industries.
References:
Acquah H. de-Graft. (2010), Comparison of Akaike information criterion (AIC) and Bayesian information criterion (BIC) in selection of an asymmetric price relationship, Journal of Development and Agricultural Economics Vol. 2(1) pp. 001-006, January, 2010
Agarwal, R.N. (2001), Technical efficiency and productivity growth in the central public sector enterprises in India during 1990s, Discussion Paper No.28/2001, Institute of Economic Growth, New Delhi.
Aghion, Philippe; Blundell, Richard; Griffith, Rachel; Howitt, Peter and Prantl, Susanne (2006).“The Effects of Entry on Incumbent Innovation and Productivity”. NBER Working Paper 12027
Aitken Brian and Harrison Ann (1999). „Do Domestic Firms Benefit from FDI? Evidence from Venezuela“. American Economic Review 89
Ahluwalia, I.J.1985, Industrial Growth in India, Oxford University Press, Delhi.
Ahluwalia, M.S. (2002), Economic reforms in India since 1991: has gradualism worked? Journal of Economic Perspectives, 16(3), pp. 67-88.
Akaike H (1973). Information Theory and an Extension of the Maximum Likelihood Principle. In: B.N. Petrov and F. Csaki (eds.) 2nd International Symposium on Information Theory: 267-81 Budapest: AkademiaiKiado.
Balasubramanyam, V. N., M. Salisu and D. Sapsford (1999). “Foreign Direct Investment as an Engine of Growth,” The Journalof International Trade & Economic Development, 8,1, 27 40.
Banga, R. (2005) Impact of Liberalization on Wages and Employment in Indian Manufacturing Industries, Working Paper No. 153, New Delhi: ICRIER.
Banker, R.D., Charnes, A., and Cooper, W.W. (1984), Some models for estimating technical and scale inefficiencies in data development analysis, Management Science, 30(9), pp.1078-1092.
Besley, T. and Burgess, R. (2004), Can labor regulation hinder economic performance? Evidence from India, The Quarterly Journal of Economics, 119(1), pp.91-134.
Bitzer, Jurgen and Görg, Holger (2005).“The Impact of FDI on Industry Performance“. University of Nottingham (unpublished manuscript)
Benfratello, Luigi and Sembenelli, Alessandro (2005). “Foreign Ownership and Productivity: Is the Direction of Causality so Obvious?”. University of Torino (unpublished manuscript)
Bhandari, A. K., and Maiti, P. (2007a), “Efficiency of Indian Manufacturing Firms: Basic Metal Industry as a Case Study”, International Journal of Business and Economics, 6 (1), 71-88.
Bhandari, A. K., and Ray, S. C. (2007b), “Technical Efficiency in the Indian Basic Metals Industry: A Nonparametric Analysis of Firm-Level Data”, Department of Economics .Working Paper Series: 49, University of Connecticut, USA.
Bickel.P, Zhang.P (1992).Variable selection in nonparametric regression with categorical covariates. J. Am. Stat. Assoc. 87: 90–97.
Bozdogan.H (1987). Model Selection and Akaike’s Information Criterion (AIC): The General Theory and Its Analytical Extensions. Psychometrika (52)3: 345-370.
Borensztein E. and J. Ostry (1996), “Accounting for China’s Growth Performance,” American Economic Review, Vol. 86, No.2, 224-28.
Brahmananda, P.R.(1982): Productivity in Indian Economy: Rising inputs for falling outputs. Himalaya Publishing House.
Broadman H. G. and X. Sun (1997), “The Distribution of Foreign Direct Investment in China”, The World Economy, Vol. 20, No. 3, May, 339-361.
Chen C. H. (1996), “Regional determinants of foreign direct investment in Mainland China”, Journal of Economic Studies, Vol. 23, No. 2, 18-30.
Chow G. C. (1993), “Capital Formation and Economic Growth in China,” Quarterly Journal of Economics, Vol. 103, No. 3, 809-42.
Coughlin C. C. and E. Segev (2000), “Foreign Direct Investment in China: A Spatial Econometric Study”, The World Economy, Vol. 23, No. 1, January, 1-23.
Démurger S. (1996a), “Différencesrégionales de la croissanceindustrielle en Chine”, Revue d’Economie du Développemnt, No. 1-2, June.
Démurger S. (1996b), “On the role of openness in the Chinese industrial growth process: A city-level assessment”, Étudeset Documents, Ec.96.04, CERDI-IDREC, Clermont-Ferrand, France.
Démurger S. (2000), Economic Opening and Growth in China, OECD Development Centre Studies, Paris, March.
Dickey, D.A., Fuller, W.A. (1979). Distribution of the estimators for the autoregressive time series with a unit root. Journal of the American Statistical Association, 74, 427-431.
Dickey, D.A., Fuller, W.A. (1981). Distribution of the estimators for the autoregressive time series with a unit root.Econometrica, 49, 1057-1072.
Driffield, N.L. and Kambhampati ,U.S. (2003), Trade liberalization and the efficiency of firms in Indian manufacturing, Review of Development Economics, 7(3), pp.419-430.
Elliott, Graham, Rothenberg, Thomas J., and James H. Stock.(1996) Efficient Tests for an Autoregressive Unit Root. Econometrica, 64:4, pp.813-836.
Engle, R. F.,&Granger, C.W. J. (1987). Cointegration and error correction: representation, estimation, and testing. Econometrica, 251–276.
Färe, R. and Lovell, C.A.K. (1978), Measuring the technical efficiency of production, Journal of Economic Theory, 19(1), pp.150-162.
Färe, R., Grosskopf,S. Lindgren, B. and Roos P. (1992), Productivity changes in Swedish pharmacies 1980-1989: a non-parametric Malmquist approach, Journal of ProductivityAnalysis, 4, pp.85-101.
Färe, R., Grosskopf, S. Norris, M. and Zhang Z. (1994), Productivity growth, technical progress and efficiency change in industrialized countries, American Economic Review, 84, pp.66-83.
Farrell, M.J. (1957), The measurement of productive efficiency, Journal of the Royal Statistical Society, 120(3), pp.253-290.
Fikkert, B. and Hasan, R. (1998).Returns to scale in a highly regulated economy: evidence from Indian firms, Journal of Development Economics, 56, 51-79.
Findlay, R. (1978), “Relative Backwardness, Direct Foreign Investment and the Transfer of Technology: A Simple Dynamic Model.” Quarterly Journal of Economics, 92: 1-16.
Goldar, B. Kumari, S. (2002), ‘Import Liberalization and Productivity Growth in Indian Manufacturing Industries in the 1990s’, Working Paper E/219/2002, Institute of Economic Growth, Delhi, India.
Goldar, B. (2004), Productivity trends in Indian manufacturing in the pre and post reform periods, Working Paper No.137, Indian Council for Research on International Economic Relations (ICRIER), New Delhi, India.
GörgHolger and Kerekes Monika (2005).“Does FDI Transfer Technology Across Borders.A Reexamination”. Free University of Berlin Discussion Paper No. 2005/7
Granger, C. W.J., (1969), “ Investigation Causal Realtions by Econometrics Model and Cross Spectral Methods”, Econometrica, 37, 424-438
Griliches, Z and Y. Ringstad (1971), Economics of scale and the form of the production function, North Holland, Amsterdam
Hu, Chan G and Bharat Trehan., (1995), “ Modeling the Time Series Behaviour of the Aggregate Wage Rate”, Federal Reserve Bank of San Francisco, Economic Review, 3-13.
Kalirajan, K.P. and Shand, R.T. (1999), Frontier production functions and technical efficiency measures, Journal of Economic Surveys, 13(2), pp.149-172.
Kalirajan, K.P., and Shand, R.T. (2001), Technology and farm performance: paths of productive efficiencies over time, Agricultural Economics, 24(3), pp.297-306.
Lin J. Y., F. Cai and Z. Li (1996), The China Miracle, The Chinese University Press, Hong Kong.
Lovell, K.C.A. (1996), Applying efficiency measurement techniques to the measurement of productivity change, Journal of Productivity Analysis, 7, pp.329-340.
Mody A. and F. Y. Wang (1997), “Explaining Industrial Growth in Coastal China: Economic Reforms... and What Else?”, The World Bank Economic Review, Vol. 11, No. 2, May, 293-325.
Mitra, A. (1999), Total factor productivity growth and technical efficiency in Indian industries, Economic and Political Weekly, Vol.34 No.31, pp.
Mitra A., A. Varoudakis and M-A.Véganzonès (1998), “State Infrastructure and Productive Performance in Indian Manufacturing”, OECD Technical Paper, 139, August, Paris.
Krishna, P. and Mitra, D. (1998), Trade liberalization, market discipline and productivity growth: new evidence from India, Journal of Development Economics ,56(2), 447-462.
Kumar Sunil., (2012), “Regional Variations in Labor Productivity Growth in Indian Manufacturing Sector”. Anvesak, 32(2), 111 – 136
Mukherjee, D. and Majumder, R. (2007), Efficiency, technological progress and regional comparative advantage: a study of the organized manufacturing sector in India, Asia-Pacific Development Journal, 14(2), pp.23-54.
Mukherjee, K. and Ray, S.C. (2005), Technical efficiency and its dynamics in Indian manufacturing: an inter-state analysis, Indian Economic Review, 40(2), 101-125.
Nehru V. and A. Dhareshwar (1994), “New Estimates of Total Factor Productivity Growth for Developing and Industrial Countries”, World Bank Policy Research Working Paper, No. 1313, June.
Onder, O.A., Deliktas, E. and Lenger, A. (2003), Efficiency in the manufacturing industry of selected provinces in Turkey: a stochastic frontier analysis, Emerging Markets Financeand Trade, 39(2), pp.98-113.
Page, J.M. (1984), Firm size and technical efficiency: applications of production frontiers to Indian survey data, Journal of Development Economics, 16(1), 129-152.
Patibandla, M. (1998), Structure, organizational behavior, and technical efficiency: the case of an Indian industry, Journal of Economic Behavior& Organization, 34(3), 419-434.
Pattnayak, S.S. and Thangavelu S.M. (2005), Economic reform and productivity growth in Indian manufacturing industries: an interaction of technical change and scale economies, Economic Modelling, 22(4), 601-615.
Phillips, P.C.B. and P. Perron (1988). “Testing for Unit Roots in Time Series Regression,” Biometrika, 75, pp.335-346.
Pindyck, Robert S and D.L.Rubinfeld., (1998), “ Econometrics Model and Economic Forecasts” Irwin McGraw-Hill, Singapore.
Schwarz G (1978). Estimating the Dimension of a Model. Annals of Statistics 6: pp.461–464.
Solow, R.M. (1956), “A Contribution to the Theory of Economic Growth”, The Quarterly Journal of Economics, Vol. 70, No. 1. (Feb., 1956), pp. 65-94.
Sun H. (1998), Foreign Investment and Economic Development in China: 1979-1996, Ashgate.
Sun H., P. Hone and H. Doucouliagos (1999), “Economic openness and technical efficiency”, Economics of Transition, Vol. 7, No. 3, 615-636.
Taymaz, E. and Saatci, G. (1997), Technical change and efficiency in Turkishmanufacturing industries, Journal of Productivity Analysis, 8, pp.461-475.
Unel, B. (2003), Productivity trends in India’s manufacturing sectors in the last two decades, Working Paper No.03/22, International Monetary Fund (IMF), USA.
UNCTAD (1999). World Investment Report 1999.
UNCTAD (2005).World Investment Report 2005.“Transnational Corporations and the Internationalization of R&D.”
Wei S. J. (1994), “The Open Door Policy and China’s Rapid Growth: Evidence from City-Level Data”, in T. Ito and A. O. Krueger (eds.), Growth Theories in Light of the East AsianExperience, The University of Chicago Press, Chicago and London.
Wei S. J. (1996): “Foreign Direct Investment in China: Sources and Consequences”, in T. Ito and A. O. Krueger, Financial Deregulation and Integration in East Asia, NBER, The University of Chicago Press.
Wei Z. B., O. Varela and M. K. Hassan (2002), "Ownership and performance in Chinese manufacturing industry", Journal of Multinational Financial management, 12, 61-78.
World Bank (1997), World Development Report 1997: The State in a Changing World, New York: Oxford University Press.
Zhang F. and J. Zheng (1998), “The Impact of Multinational Enterprises on Economic Structure and Efficiency in China”, China Centre for Economic Research, Discussion Paper No. E1998007.
Zhang.P (1993).On the convergence of model selection criteria.Comm.Stat.-Theory Meth. 22: pp.2765-2775.