Hedge Ratio and Hedging Horizon: A Wavelet Based Study of Indian Agricultural Commodity Markets

Dr. Irfan ul Haq Lecturer Department of Commerce Govt. Degree College Shopian (Jammu and Kashmir) Email: fanpin20@gmail.com

Abstract

In India the history of commodity derivatives market has a long history, though a structured and exchange traded derivative trading is not more than a decade long. The derivatives market is established for the main purpose of hedging the price risk. Since the inception of derivatives, the concern of how much to hedge technically called the hedge ratio is widely debated and discussed. In present paper, we has empirically estimated the hedge ratio using three different methodologies viz. OLS, ECM and WAVELET Approach for ten agricultural commodities traded on NCDEX platform. The results witnessed reveal that wavelet hedge ratio is comparatively larger than OLS and ECM, and as we go on increasing the hedging horizon hedge ratio increases.

Keywords: Derivatives, Price risk, Hedging horizon

Introduction

Futures market has an important function of hedging the price risk faced by producers, traders and other stake holders. The concept of Hedging strategy is based on compensating anticipated spot market losses with the gains from the futures market. In order to execute hedging strategy one has to take opposite position in futures market with respect to the position in spot market.

Most studies in hedging are related to hedge ratio. It is either estimation of optimal hedge ratio or optimal hedge ratio derivation based on certain objective functions. The derivation is mostly based on maximization of expected utility or minimization of return variance. The empirical estimation of hedge ratio varies in terms of different methodologies used. The present study focuses on estimating the optimal hedge ratio based on tradition and new wavelet methodology to find out the optimal hedge ratio for different time horizons.

The estimation of optimal hedge ratio generally differs in the methodologies used. The most common methodologies vary from simple ordinary least square (e.g Ederington, 1979, ; Malliaris & Urrutia, 1991; Benet, 1992) to more complex ones like ARCH and GARCH methods (Cecchetti, Cumby, & Figlewski, 1988; Baillie & Myers, 1991; Sephton, 1993) , Cointegration Method (Ghosh, 1993; Lien & Luo, 1993; Geppert, 1995; Chou, & Lee, 1996), the random coefficient method (Grammatikos & Saunders, 1983) , cointegration - heteroscadestic method (e.g., see Kroner & Sultan, 1993) and wavelet method (Lien and Shrestha,20007).

However, the problem with most of the empirical studies is they ignore the hedging horizon which is different for different participants in the market. With the increase in hedging horizon the optimal hedge ratios tends to increase as witnessed by many researchers [2] . In this article, we have decomposed the original time series of futures and spot prices into different horizons using wavelet methodology. The advantage with wavelets is that the sample size is not reduced while matching the hedging horizon and data frequency.

Methodology

Hedge ratio is defined as the ratio of value of futures contracts to the value of the underlying asset. Optimal hedge ratio is the ratio that eliminates or minimizes the price risk. While hedging through the identical asset as underlying, the number of contracts that are booked to cover the long or short positions is equal to the exposure in the underlying asset. In such a case it is implicitly set the hedge ratio equal to one, which is regarded as optimum.

The optimum hedge ratio (value of futures contracts to the value of the underlying asset) is dependent upon the degree of correlation between the spot prices and the futures prices. For a hedge through futures the optimum hedge ratio is that ratio which minimizes the risk of the combined portfolio of the underlying and the futures.

If h is the futures contracts booked then the risk of the combined portfolio of the underlying asset and the futures is given by variance of the return from the portfolio so constructed.

Return from the portfolio = (1)

Variance of the portfolio, V =

=

For minimization of the variance of the portfolio, .

Therefore, (2)

Where = optimal hedge ratio

= Correlation coefficient of spot and futures price

= Standard deviations of spot and futures prices respectively.

For the estimation of optimal hedge ratio both traditional and new methodology is used. The tradition or conventional methodologies include Ordinary Least Square (OLS) and Error Correction Model (ECM). The new methodology for time varying hedge ratio is wavelet method. All the three methodologies are discussed below;

1. Ordinary Least Square (OLS)

The traditional approach to estimate minimum variance hedge ratio is Ordinary Least Square (OLS) technique, where spot returns are regressed on futures returns. The regression equation for spot and futures returns can be expressed as;

(3)

Where, is a spot return and is futures returns. β is the minimum variance hedge ratio.

The problem with OLS is that it does not incorporate long run equilibrium, so another model, error correction is estimated to get the optimal hedge ratio.

2. Error Correction Model

Error Correction Model is one of the multiple time series model used to estimate the speed of adjustment with which dependent and independent variables return to equilibrium. Error Correction Models (ECMs) are also used to estimate the short and long run relationships between the time series. The general structure of any ECM is:

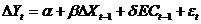(4)

Where EC is the error correction term.

In the present study the ECM model extended by Lien and Shrestha (2005) is used. The model is as;

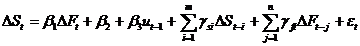(5)

Where is a residual of cointegrating equation;

(6)

is Error Correction (EC) hedge ratio.

The problem with both the conventional methods is that data frequency is to be matched with hedging horizon which will lead to smaller sample. To overcome this problem another methodology where matching of frequency data and hedging horizon is not needed is used here. This methodology is based on Wavelet Approach.

3. Wavelet Approach

The origin of Wavelets though recognized in 1980s was before put forth in 1909 by Alfred Haar and nowadays his contribution is recognized as Haar wavelets. Wavelet Analysis is groomed by the collaborative work of Ingrid Daubechies (Mathematician) and Stephane Mallat (Signal Processing Professional). Daubechies (1996) points out that wavelet is more than the sum of different ideas from different fields merged together. The different fields which contribute to Wavelet analysis include mathematics, physics, engineering, and computer science. Daubechies (1992) presented the theoretical background of wavelets but before this its application was first explored by Mallat (1989). Wavelet analysis is of two types - continuous wavelet analysis and discrete wavelet analysis. The first one assumes continuous time functions and second one assumes sampling at discrete the points which are equally spaced.

In common parlance wavelets are functions with specific properties. These functions satisfy certain mathematical requirements which find applications in representing other functions or data. Mathematically wavelets is a function over the real axis such that as .

From definition it follows that wavelet is localized in space or time i.e. with time oscillations of damp quickly to zero. This localization property of wavelets makes them interesting and useful in handling the non stationary data which changes rapidly over a period of time. A time series can be presented as wavelet functions by applying Wavelet transformation, which means a time series, can be decomposed into multi-resolution components.

Wavelets are of two types father and mother wavelets.

, (7)

In time series, father wavelet represents smooth and low frequency components and mother wavelet represents detail and high frequency components. In short we can say that father wavelets represent trend components and mother wavelets represent all deviations from trend Two scale dilution equation is used to derive the wavelets.

The dilution equation for father wavelet is

(8)

And the dilution equation for mother wavelet is

(9)

Where and are low pass and high pass coefficients respectively and are defined as;

, (10)

In practice we deal with time series rather than continuous functions. For this we employ wavelet filters which are short sequence of values and are denoted by , L represents width of the filter.

The restrictions , , (j= non zero integer)must be satisfied by (filter coefficient).

The filter coefficients and are related to each other as;

The time series can be represented in terms of wavelet coefficients as;

(11)

Or (12)

Equation (11) is a representation of time series with different time scales obtained from the decomposition of . This decomposition process is called multi resolution analysis (MRA). In case of discrete time series, discrete wavelet transform is used to perform MRA using digital filtering technique. Suppose represents a discrete time series. Then MRA leads to decomposition of as;

(13)

Discrete wavelet transforms are of two types; DWT (discrete wavelet transform) and MOWDT (maximal overlap discrete wavelet transform). DWT decomposes the original series using orthonormal transformation. Suppose represent observations of a discrete time series and N is an integer multiple of . Then column vector of discrete wavelet coefficients w under DWT is given by

(14)

W is a transformed N x N real- real valued matrix satisfying . Coefficient vector w is also divided into sub vectors , j= 1, 2……, J and as;

(15)

Vector and Vector.

and actually represent wavelet coefficient vector and scaling coefficient vector respectively.

Another transformation i.e. MOWDT involves non-orthogonal transformation which leads to J transform coefficients vectors each of length N and N is not necessarily multiple of 2. For MOWDT the coefficient vector of length (J + 1)N is given by

(16)

Where is an (J + 1)N X N matrix and

(17)

Note and are wavelet coefficient vector and scaling vector respectively.

If the data is sampled at an interval of Δt, then is associated with changes on the time scale of length (Percival and Mofjeld 1997). For example, in case of daily data, , is associated with daily time scale and is associated 2 days time scale and so on. Furthermore, is associated with length of the time scale which is equal to or longer. The limit of J is sample dependent, and is always less than log₂(N), N is the sample size.

Based on equation (11) spot and futures return time series can be decomposed into different time scales as;

(18)

(19)

Where , is the spot return series and is the futures return series.

Now using J decompositions to estimate J regressions;

(20)

where is the minimum variance hedge ratio associated with j^th time scale. Both DWT as well MODWT can be used to perform the above analysis. In this study we have used MODWT, because of its advantages over DWT.

Data

The sample of the study is ten agricultural commodities viz. Barley, Chana, Chilli, Guar Gum, Guar Seeds, Jeera, Pepper, Soy oil, Soy Bean and Turmeric. The data used in the present study is obtained from National Commodities & Derivatives Exchange Ltd (NCDEX). The data is collected for different periods based on the availability of trading cycles and contracts. A pooled series of prices for each commodity is generated by the process of roll over from one maturity to the next. Daily closing futures prices of current maturity and corresponding closing spot prices are used in the study. The detailed summary of data period for different commodities is presented in Table 1.

Results

The results of various optimal hedge ratios are provided in Tables 2 to 6. The hedge ratios are estimated for different hedging horizons viz. 2 days, 4 days, 8 days, 16 days and 32 days using three different methodologies OLS, ECM and Wavelets. The wavelet ratio exceeds both OLS and ECM ratios in almost all the cases except in the lowest scale i.e. 2 days. ECM and OLS ratios are almost similar. The wavelet ratio being highest among the three methodologies can be attributed to the fact that wavelet approach does not reduce the sample size which is quiet prominent in other two methodologies. As we go on increasing the time scale hedge ratio goes on increasing irrespective of the methodology used.

Conclusion

In Indian commodity markets, the agricultural futures trading have got momentum after the establishment of national commodity exchanges and some regulatory measures. It is important to assess the functions for which the futures markets are established. In this context this study has evaluated the optimal hedge ratios and hedging effectiveness of agricultural futures. Three different methodologies OLS, ECM and Wavelets have been employed to estimate optimal hedge ratio. The hedge ratios suggested by OLS and ECM are almost equal but wavelet hedge ratios are higher than the former two. The hedging effectiveness measured by Ederington Measure suggests good amount of hedging in Indian markets and more particularly in commodity with high trading volumes.

Table 1: Sample and Sample Size

Commodity	Data Period	No of Observations	Commodity	Data Period	No of Observations
Barley Channa Chilli Guar Gum Guar Seeds	Mar.2007to Dec 2011 Jan 2006 to Dec 2011 Feb 2006 to Dec 2011 Jan 2006 to Dec 2011 Jan 2006 to Dec 2011	805 1085 812 1289 1312	Jeera Pepper Soy Oil Soy Bean Turmeric	Jan 2006 to Dec 2011 Feb 2006 to Dec 2011 Jan 2006 to Dec 2011 Jan 2006 to Dec 2011 March 2009 to Dec 2011	1447 1665 1314 1314 481

Table 2: Optimal Hedge Ratio (2 day Returns)

Commodity	OLS	ECM	Wavelet
Barley Channa Chilli Guar Gum Guar Seeds Jeera Pepper Soy Oil Soy Bean Turmeric	0.59 0.50 0.41 0.76 0.67 0.267 0.342 0.683 0.676 0.573	0.52 0.47 0.45 0.78 0.673 0.267 0.329 0.685 0.663 0.657	0.49 0.32 0.40 0.63 0.568 0.185 0.179 0.560 0.543 0.503

Table 3: Optimal Hedge Ratio (4 day Returns)

Commodity	OLS	ECM	Wavelet
Barley Channa Chilli Guar Gum Guar Seeds Jeera Pepper Soy Oil Soy Bean Turmeric	0.64 0.48 0.42 0.75 0.673 0.263 0.348 0.685 0.656 0.604	0.52 0.48 0.42 0.76 0.663 0.256 0.327 0.677 0.655 0.597	0.68 0.6 0.41 0.84 0.731 0.302 0.406 0.741 0.746 0.607

Table 4: Optimal Hedge Ratio (8 day Returns)

Commodity	OLS	ECM	Wavelet
Barley Channa Chilli Guar Gum Guar Seeds Jeera Pepper Soy Oil Soy Bean Turmeric	0.66 0.49 0.20 0.74 0.673 0.287 0.370 0.668 0.239 0.590	0.29 0.50 0.20 0.72 0.655 0.280 0.358 0.665 0.238 0.585	0.70 0.73 0.44 0.88 0.816 0.367 0.552 0.799 0.727 0.684

Table 5: Optimal Hedge Ratio (16 day Returns)

Commodity	OLS	ECM	Wavelet
Barley Channa Chilli Guar Gum Guar Seeds Jeera Pepper Soy Oil Soy Bean Turmeric	0.86 0.51 0.44 0.738 0.684 0.269 0.370 0.700 0.680 0.600	0.57 0.53 0.44 0.729 0.661 0.267 0.358 0.696 0.681 0.588	0.73 0.66 0.47 0.920 0.843 0.463 0.644 0.799 0.792 0.717

Table 6: Optimal Hedge Ratio (32 day returns)

Commodity	OLS	ECM	Wavelet
Barley Channa Chilli Guar Gum Guar Seeds Jeera Pepper Soy oil Soy Bean Turmeric	0.92 0.46 0.45 0.74 0.915 0.291 0.363 0.682 0.652 0.262	0.57 0.47 0.45 0.74 0.913 0.282 0.349 0.676 0.657 0.374	0.94 0.83 0.69 0.98 0.897 0.531 0.754 0.963 1.005 0.866

References

Baillie, R. T., & Myers, R. J. (1991). Bivariate GARCH estimation of the optimal commodity futures hedge. Journal of Applied Econometrics,6, 109–124.

Benet, B. A. (1992). Hedge period length and ex-ante futures hedging effectiveness:The case of foreign-exchange risk cross hedges. Journal of Futures Markets, 12, 163–175.

Cecchetti, S. G., Cumby, R. E., & Figlewski, S. (1988). Estimation of the optimal futures hedge. Review of Economics and Statistics, 70, 623–630.

Chen, S. S., Lee, C. F., & Shrestha, K. (2001). On a mean-generalized semivariance approach to determining the hedge ratio. Journal of Futures Markets, 21, 581–598.

Chen, S. S., Lee, C. F., & Shrestha, K. (2004). Empirical analysis of the relationship between the hedge ratio and hedging horizon: A simultaneous estimation of the short- and long-run hedge ratios. Journal of Futures Markets, 24, 359–386.

Chou, W. L., Fan, K. K., & Lee, C. F. (1996). Hedging with the Nikkei index futures: The conventional model versus the error correction model. Quarterly Review of Economics and Finance, 36, 495–505.

Ederington, L. H. (1979). The hedging performance of the new futures markets.Journal of Finance, 34, 157–170.

Gencay, R., Selcuk, F., & Whitcher, B. (2002). An introduction to wavelets and other filtering methods in finance and economics. New York: Academic Press.

Geppert, J. M. (1995). A statistical model for the relationship between futurescontract hedging effectiveness and investment horizon length. Journal of Futures Markets, 15, 507–536.

Ghosh, A. (1993). Hedging with stock index futures: Estimation and forecasting with error correction model. Journal of Futures Markets, 13, 743–752.

Grammatikos, T., & Saunders, A. (1983). Stability and the hedging performance of foreign currency futures. Journal of Futures Markets, 3, 295–305.

Hill, J., & Schneeweis, T. (1982). The hedging effectiveness of foreign currency futures. Journal of Financial Research, 5, 95–104.

Kroner, K. F., & Sultan, J. (1993). Time-varying distributions and dynamic hedging with foreign currency futures. Journal of Financial and Quantitative Analysis, 28, 535–551.

Lien, D., & Luo, X. (1993). Estimating multiperiod hedge ratios in cointegrated markets. Journal of Futures Markets, 13, 909–920.

Lien, D., & Shrestha, K. (2005). Estimating the optimal hedge ratio with focus information criteria. Journal of Futures Markets, 25, 1011–1024.

Lien & Shrestha (2007). An Empirical Analysis of the Relationship between Hedge Ratio and Hedging Horizon using Wavelet Analysis. Journal of Futures Markets, 27, 127–150.

Lien, D., & Tse, Y. K. (2000). A note on the length effect of futures hedging. Advances in Investment Analysis and Portfolio Management, 7, 131–143.

Lien, D., & Tse, Y. K. (2002). Some recent developments in futures hedging. Journal of Economic Surveys, 16, 357–396.

Malliaris, A. G., & Urrutia, J. L. (1991). The impact of the lengths of estimation periods and hedging horizons on the effectiveness of a hedge: Evidence from foreign currency futures. Journal of FuturesMarkets, 3, 271–289.

Percival, D. B., & Mofjeld, H. O. (1997). Analysis of subtidal coastal sea level fluctuations using wavelets. Journal of the American Statistical Association, 92, 868–880.

Sephton, P. S. (1993). Optimal hedge ratios at the Winnipeg commodity exchange. Canadian Journal of Economics, 26, 175–193.